Question

Find m <ABC (7x-1) (3x-9

Answer 1

(7x-1)+(3x-9)=180
10x-10=180
Add 10 to both sides
10x=170
Divide both sides by 10
X=17 degrees

3x-9
3(17)-9
51-9
=48

Answer 2

Therefore,
`\angle ABC = 48\degree`

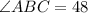
Explanation:

We need to find the
`\angle ABC`

Since,
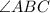
`\angle DBC = 180\degree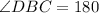` ( since DBC is straight line )

`(7x-1)+(3x-9)=180\degree`

`10x-10=180 \degree`

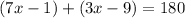
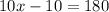
Add both the sides by 10 in above expression

`10x-10+10=180\degree+10`

`10x=180 \degree+10`

`10x=190 \degree`

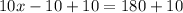
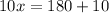
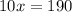
divide both the sides by 10 in above expression

`x=(190)/(10)`

`x=19`

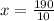
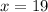
Hence, the value of x is 19.

Now, we will calculate
`\angle ABC`

`\angle ABC = 3x-9`

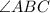
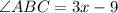
Put x = 19 in above

`\angle ABC = 3(19)-9`

`\angle ABC = 57-9`

`\angle ABC = 48`

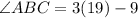
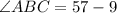
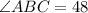
Therefore,
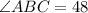`\angle ABC = 48`.