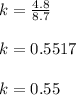Answer with explanation:
Mean (
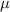 ) = 43.8
) = 43.8
Standard Deviation (
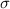 ) = 8.7
) = 8.7
We can draw the normal curve and then show where these values lie.
Or we can use the equation,
 , use positive sign when ,number is greater than mean, and negative sign when number is smaller than mean, to find that , how many standard deviations of the mean do the values 60, 40, 35, 45, and 39 fall.
, use positive sign when ,number is greater than mean, and negative sign when number is smaller than mean, to find that , how many standard deviations of the mean do the values 60, 40, 35, 45, and 39 fall.
1.→ 43.8 +8.7 k= 60
8.7 k= 60 - 43.8
8.7 k= 16.2
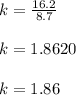
2.→ 43.8 - 8.7 k=40
43.8-40 = 8.7 k
8.7 k= 3.8
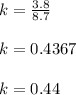
3.→43.8 - 8.7 k=35
43.8-35 = 8.7 k
8.7 k= 8.8
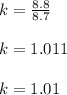
4.→43.8 + 8.7 k=45
43.8-45 = -8.7 k
-8.7 k= -1.2
8.7 k= 1.2
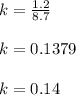
5.→43.8 -8.7 k=39
43.8-39 = 8.7 k
8.7 k= 4.8