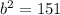Question

In triangle ABC, a = 9, c = 5, and B = 120°. Find b2.

61
83.5
128.5
151

Answer 1

Option D)
`b^2 = 151`

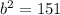
Explanation:

We are given the following information in the question:

`\triangle ABC\\\text{Side } a = 9\text{ units}\\\text{Side } c = 5\text{ units}\\\angle ABC = 120^(\circ)`

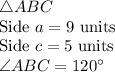
We have to find
`b^2`

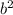
The law of cosines state that if a, b and c are the sides of triangle and b is the side opposite to angle B, then,

`b^2 = a^2 + c^2 - 2ac~\cos(B)`

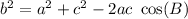
Putting the values, we have,

`b^2 = (9)^2 + (5)^2 - 2(9)(5)~\cos(120)\\\\b^2 = 81 + 25 - 90(-0.5)\\\\b^2 = 151`

Option D)
`b^2 = 151`

Answer 2

The correct answer is 151.

Explanation:

Given,

In triangle ABC,

BC = a = 9 unit,

AB = c = 5 unit,

m∠B = 120°,

We have to find : b² or AC²,

By the cosine law,

`b^2=a^2+c^2-2ac cosB`

`=9^2+5^2-2* 9* 5* cos 120^(\circ)`

`=81+25-90* -0.5`

`=81+25+45`

`=151`

Hence, the value of
`b^2` is 151.