Let

using a graphing tool
see the attached figure to better understand the problem
we know that
Parallelogram is a quadrilateral with opposite sides parallel and equal in length
so
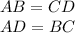
The area of a parallelogram is equal to
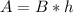
where
B is the base
h is the height
the base B is equal to the distance AB
the height h is equal to the distance AE
Step 1
Find the distance AB
the formula to calculate the distance between two points is equal to
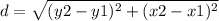
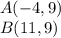
substitute the values
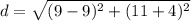
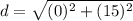
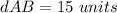
Step 2
Find the distance AE
the formula to calculate the distance between two points is equal to
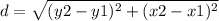

substitute the values
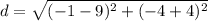
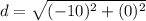

Step 3
Find the area of the parallelogram
The area of a parallelogram is equal to
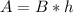
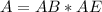
substitute the values
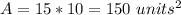
therefore
the answer is
the area of the parallelogram is
