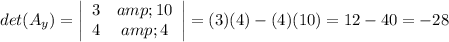Answer:
Given the system of equations, what is the value of the system determinant? x + y = 8
x - y = 10
C. -2
Given the system of equations, what is the value of the y-determinant?
3x + y - 10 = 0
4x - y - 4 = 0
A. -28
Explanation:
The determinant of the system is the determinant of the matrix formed with the coefficients of the system, usually, this matrix is called A.
![A=\left[\begin{array}{cc}1&1\\1&-1\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/high-school/5msjltpntqu67j8v60c83oxjg9abzb4z2x.png)
In the 2x2 matrix, the determinant is calculated by obtaining the difference between the diagonally down product and the diagonally up product.
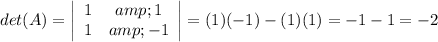
The y-determinant is the determinant of the matrix
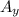 , this matrix is formed substituting in the matrix A the coefficients of y with the constant terms.
, this matrix is formed substituting in the matrix A the coefficients of y with the constant terms.
![A_y=\left[\begin{array}{cc}3&10\\4&4\end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/high-school/g0pfaphudsr0f39yid5cpkv4vlxvh06ugf.png)