Answer:
f(x) intersect the x-axis ate ( 4 , 0 ) and ( -1/3 , 0)
Explanation:
Given function,
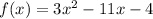
We need to find this function cuts x-axis at what point.
let,

We know that points on x-axis has y-coordinate equal to 0.
So, we put y = 0 to find value of x.
By putting y = 0, we get
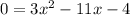

solving by quadratic formula,
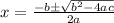
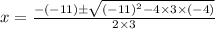
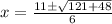
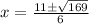
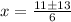


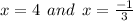
Therefore, f(x) intersect the x-axis ate ( 4 , 0 ) and ( -1/3 , 0)