Part A
If 4 candidates were to be selected regardless of gender, that means that 4 candidates is to be selected from 12.
The number of possible selections of 4 candidates from 12 is given by
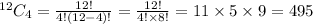
Therefore, the number of
selections of 4 candidates regardless of gender is 495.
Part B:
If 4 candidates were to be selected such that 2 women must be selected, that means that 2 men candidates is to be selected from 8 and 2 women candidates is to be selected from 4.
The number of possible selections of 2 men candidates from 8 and 2 women candidates from 4 is given by

Therefore, the number of selections of 4 candidates such that 2 women must be selected is 168.
Part 3:
If 4 candidates were to be selected such that at least 2 women must be selected, that means that 2 men candidates is to be selected from 8 and 2 women candidates is to be selected from 4 or 1 man candidates is to be selected from 8 and 3 women candidates is to be selected from 4 of no man candidates is to be selected from 8 and 4 women candidates is to be selected from 4.
The number of possible selections of 2 men candidates from 8 and 2 women candidates from 4 of 1 man candidates from 8 and 3 women candidates from 4 of no man candidates from 8 and 4 women candidates from 4 is given by

Therefore, the number of selections of 4 candidates such that at least 2 women must be selected is 201.