Alright, let's start by giving some notation to "an angle." We'll use the Greek letter

to denote it.
Next, we'll need to review a few definitions:
- Two
supplementary angles add up to a straight angle, or 180°
- Two
complementary angles add up to a right angle, or 90°
-
Trisecting an angle is splitting a larger angle into
three equal smaller angles.
If we call

's supplement
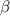
and

's complement
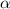
, we know that:
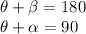
or, if we want to put everything in terms of

:
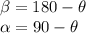
We're given from the problem that
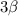
is being subtracted from
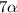
, which in terms of

gives us:
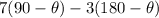
Next, we're told that this expression is equal to the angle obtained by
trisecting a right angle. A right angle is equal to 90°, so trisecting it, we get the angle 90°/3 = 30°.
Putting everything together, we have:
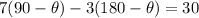
From there, solve for

, but remember that the question asks for the
supplement of

, not

itself. Fortunately, we have an equation from earlier for the supplement,
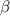
:
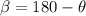
Simply put your result from solving for

into that equation and solve, and you'll have your answer.