Question

If f(x)=2−x12 and g(x)=x2−9, what is the domain of g(x)÷f(x)?

Answer 1

`\bf \begin{cases} f(x)=2-x^(12)\\ g(x)=x^2-9\\ g(x)/ f(x)=(g(x))/(f(x)) \end{cases}\implies \cfrac{x^2-9}{2-x^(12)}`

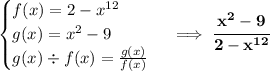
now, for a rational expression, the domain, or "values that x can safely take", applies to the denominator NOT becoming 0, because if the denominator is 0, then the rational turns to undefined.

now, what value of "x" makes this denominator turn to 0, let's check by setting it to 0 then.


`\bf 2-x^(12)=0\implies 2=x^(12)\implies \pm\sqrt[12]{2}=x\\\\ -------------------------------\\\\ \cfrac{x^2-9}{2-x^(12)}\qquad \boxed{x=\pm \sqrt[12]{2}}\qquad \cfrac{x^2-9}{2-(\pm\sqrt[12]{2})^(12)}\implies \cfrac{x^2-9}{2-\boxed{2}}\implies \stackrel{und efined}{\cfrac{x^2-9}{0}}`

so, the domain is all real numbers EXCEPT that one.