Question

Can someone help answer and explain to me how to solve this? log (lowercase 6) 1/36

Answer 1

㏒₆
`(1)/(36)`
so 6² = 36
therefore, 6⁻² =
`(1)/(36)`

so your answer will be -2
the power is the answer

Answer 2

Answer: The log simplifies to -2

-------------------------------------------
-------------------------------------------

Step-by-step explanation:

We will use the log rule that log(x^y) = y*log(x). Call this log rule 1. This log rule basically allows us to pull the exponent down.

Another log rule that we will use is
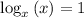
`\log_x\left(x\right) = 1` where x is any positive real number but x = 1 is NOT allowed. Call this log rule 2.

Because 36 = 6^2, this means that 1/36 = 6^(-2)

-------------

So,


`\log_6\left((1)/(36)\right)=\log_6\left((1)/(6^2)\right)`


`\log_6\left((1)/(36)\right)=\log_6\left(6^(-2)\right)`


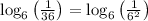
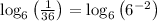
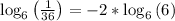
`\log_6\left((1)/(36)\right)=-2*\log_6\left(6\right)` Use log rule 1 (see above)


`\log_6\left((1)/(36)\right)=-2*1` Use log rule 2 (see above)


`\log_6\left((1)/(36)\right)=-2`

This means that the given expression simplifies to -2

You can use a calculator to type in "log(1/36)/log(6)" without quotes and you should get -2 as the answer