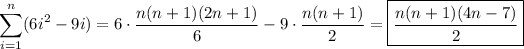Question

given the quadratic pattern -3,6,27,60 show that the sum of the first n ,at the pattern can be given by Sn=6n²+3n​

Answer 1

The given solution is not correct...

Let a(n) be the n-th term in the sequence. Since a(n) is quadratic, we know that we can write

a(n) = b n² + c n + d

for some constants b, c, d.

Using the given known values of a(n), we then have

a(1) = b + c + d = -3

a(2) = 4b + 2c + d = 6

a(3) = 9b + 3c + d = 27

Solve these equations for b, c, and d.

• Eliminate d from the first two equations:

(4b + 2c + d) - (b + c + d) = 6 - (-3) ⇒ 3b + c = 9

(9b + 3c + d) - (b + c + d) = 27 - (-3) ⇒ 8b + 2c = 30

• Eliminate c from the two new equations and solve for b :

(8b + 2c) - 2 (3b + c) = 30 - 2(9) ⇒ 2b = 12 ⇒ b = 6

• Solve for c and d :

3b + c = 3(6) + c = 9 ⇒ c = -9

b + c + d = 6 - 9 + d = -3 ⇒ d = 0

So, a(n) = 6n² - 9n.

The sum of the first n terms of this sequence is

`\displaystyle \sum_(i=1)^n a(i) = \sum_(i=1)^n (6i^2 - 9i)`

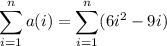
Recall the formulas for sums of powers,

`\displaystyle \sum_(i=1)^n i = \frac{n(n+1)}2`

`\displaystyle \sum_(i=1)^n i^2 = \frac{n(n+1)(2n+1)}6`

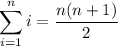
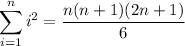
Then the sum we want is

`\displaystyle \sum_(i=1)^n (6i^2 - 9i) = 6\cdot\frac{n(n+1)(2n+1)}6 - 9\cdot\frac{n(n+1)}2 = \boxed{\frac{n(n+1)(4n-7)}2}`