The inverse function gives us -1 when x = 3.
In order to find this, we have to solve for the inverse. We do this by switching the x and f(x) values and then you can solve for the new f(x) value. The work for this is done below.
f(x) = 4(x + 3) - 5 ----> Switch the x and f(x)
x = 4(f(x) + 3) - 5-----> Add 5 to both sides.
x + 5 = 4(f(x) + 3) ----> Divide both sides by 4.
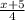 = f(x) + 3 ---> Subtract 3 from both sides.
= f(x) + 3 ---> Subtract 3 from both sides.
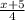 - 3 = f(x)
- 3 = f(x)
Now that you've returned to f(x), you have the inverse. Now we can take the inverse equation and plug in for x = 3.
f(x) =
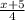 - 3
- 3
f(3) =
 - 3
- 3
f(3) =
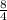 - 3
- 3
f(3) = 2-3
f(3) = -1