Answer:
1) 8
2) 5
3) False
4) Option B
Explanation:
1) We have to find the remainder when we divide (x² + 4) by (x - 2)
To get the remainder we will put x = 2 in (x² + 4)
= (2)² + 4
= 8
2). We have to evaluate f(-1) using substitution in f(x) = 2x³ - 3x² - 18x - 8
f(-1) = 2(-1)³ - 3(-1)²- 18(-1) - 8
= 2(-1) - 3 + 18 -8
= -2 - 3 + 18 - 8
= 5
3) The point (1, 0) lies on the graph of p(x) =
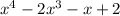
If this point lies on the graph then p(1) should be equal to zero.
p(1) = 1³ - 7(1)² + 7(1) - 9
= 1 - 7 + 7 - 9
= -8 ≠ 0
Therefore, It's false.
4). (x - 1) is a factor of p(x) = x³ - 7x² + 15x - 9
Now we will factorize it further when (x - 1) is a zero factor.
By Synthetic division
1 | 1 - 7 15 -9
1 -6 9
-----------------------------
1 -6 9 0
Now we have got the expression as (x - 1)(x²- 6x + 9)
Or (x -1)(x² - 6x + 9) = (x - 1)(x - 3)(x - 3)
Therefore, Option B. is the answer.