Answer:
The answer is

Explanation:
In order to determine the slope-intercept form equation, we need to know the formula. The formula needs a slope (m) and a point (x,y) that belongs to the equation.
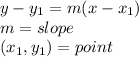
For m:
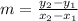
So, first we have to define every variable and then we replace them into the formula:
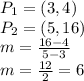
It doesn't matter the order of how you define the points. The result will be the same.
Then:
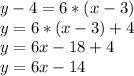
Finally, the slope-intercept form equation is
