ANSWER
The missing term is
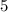
Step-by-step explanation
The quadratic expression given to us is

We factor 3 to obtain,
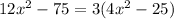
We rewrite the expressions in the parenthesis to obtain,
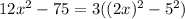
Recall that,

We apply the difference of two squares formula for the expression in the parenthesis to obtain,
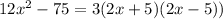
By comparing to,
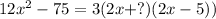
The missing term is 5.