Question

What is the length of line RS? Use the law of sines to find the answer.Round to the nearest tenth.

Answer 1

Answer: The length of RS = 2.4 (nearest tenth)

Answer 2

Refer to the diagram below.

Let x = length of line segment RS.
Let Q = ∠RQS.
Let S = ∠RSQ

According to the Law of Sines,

`(sinS)/(2.4) = (sin80^(o))/(3.1) \\\\sinS = ((2.4)/(3.1)) sin 80^(o)= 0.7624 \\\\ S = sin^(-1)0.7624 = 49.68^(o)`

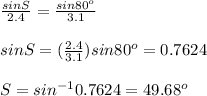
Because the sum of angles in a triangle is 180°, therefore
∠Q = 180 -(80 + 49.68) = 50.32°

Apply the Law of Sines again to obtain

`(x)/(sinQ) = (3.1)/(sin80^(o)) \\\\ x = ( (sin50.32^(o))/(sin80^(o)))3.1 = 2.423`

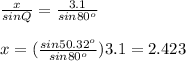
Answer: The length of RS = 2.4 (nearest tenth)