Answer:
It is increased by 100%. The numerator is two times more than the denominator. That's why original fraction will become
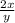 .
.
Explanation:
We need to find the percentage, if its numerator is increases by 60% and its denominator decreases by 20%.
First, we let the original fraction:

We have given its numerator is increases by 60% and denominator is decreases by 20% then,
New fraction will become =
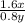 .
.
Divide the new fraction by original fraction, then we get:
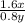 /
/

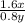 *
*

Then, it will become
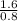 .
.
We can see that, The numerator is two times more than the denominator. That's why original fraction will become
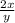 .
.
It is increased by 100%.
If we take an example, Suppose the original fraction is
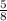 and the new fraction will become
and the new fraction will become
 .
.
=
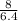 =
=
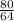
=
 , it is twice of original fraction
, it is twice of original fraction
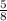 .
.