Answer:
The correct option is D. The interval [2.5, 4] contains a local minimum for the graphed function
Explanation:
According to the definition of local mimima, a function has local minima at c if
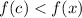
for all values of x. where,
![x\in [c-\epsilon, c+\epsilon]](https://img.qammunity.org/2018/formulas/mathematics/high-school/qiov9fpeca1bcb8mug2zulsfdhcozp05ig.png)
From the graph it is clear that the given function has local minima at (-0.44,-4.3) and (3,-4).
![-0.44\\otin [-4, -2.5], 3\\otin [-4, -2.5]](https://img.qammunity.org/2018/formulas/mathematics/high-school/4t4zs5eg5v5vz73ms3d23ualqtmwpodnhk.png)
Therefore option A is incorrect.
![-0.44\\otin [-2, -1], 3)\\otin [-2, -1]](https://img.qammunity.org/2018/formulas/mathematics/high-school/kvqxsgqhlvmxh7i9stvo6c6wc02lb84w5w.png)
Therefore option B is incorrect.
![-0.44\\otin [1, 2], 3\\otin [1, 2]](https://img.qammunity.org/2018/formulas/mathematics/high-school/q6xmizvffpcmoc06yaga9noyviak5054om.png)
Therefore option C is incorrect.
![-0.44\\otin [2.5, 4], 3\in [2.5, 4]](https://img.qammunity.org/2018/formulas/mathematics/high-school/r0ljf9xfwws3qbtg7w54js33glsxpm7nxh.png)
Therefore option D is correct.