Answer:
The length of the diagonal of the given Rectangle is, 11.80 m (Approx.)
Explanation:
In Rectangle:
* It is a four sided shape where every angle is a right angle.
* The alternative sides are equal.
*Two axes of symmetry bisect each other.
* Diagonals are equal in length.
The figure of rectangle has given the length
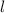 = 10m
= 10m
In right angle triangle ADC.
DC = 10 m ( as alternative sides are equal )
Note that we are given here the adjacent and we have to find the length of hypotenuse, then we use trigonometric ratio that contains both sides adjacent and hypotenuse.
Use:
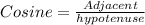
then,
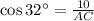 or
or
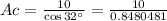
On simplify we get;
AC = 11.791784 m
therefore, the length of the diagonal of this rectangle (AC) is, 11.80 m (Approx)