By the 6 trigonometric ratios in a right triangle
(sine, cosine, tangent, cotangent, secant, cosecant)
we have the following:
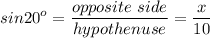
So,
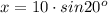
sin20° must be given, or can be found using a calculator:
Using the calculator of our pc: Calculator- view:Scientific- press 20 then sin button, we find : sin20°=0.342
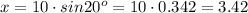
Answer: A)3.4