Question

Find the height of the triangle


10 points!

Answer 1

A. 3.4

Step-by-step explanation:

We have been given a graph of a right triangle and we are asked to find the height of our given right triangle.

Since we know that sine relates the opposite side of a right triangle to hypotenuse, so we will use sine to find height of our given triangle.

`\text{Sin}=\frac{\text{Opposite}}{\text{Hypotenuse}}`

`\text{Sin}(20^(o))=\frac{\text{Opposite}}{\text{Hypotenuse}}`

`\text{Sin}(20^(o))=(x)/(10)`

`0.342020143326=(x)/(10)`

`0.342020143326* 10=(x)/(10)* 10`

`0.342020143326* 10=x`

`x=03.42020143326\approx 3.4`

Therefore, the height of our given triangle is 3.4 units and option A is the correct choice.

Answer 2

By the 6 trigonometric ratios in a right triangle

(sine, cosine, tangent, cotangent, secant, cosecant)

we have the following:



`\displaystyle{ sin20^o= (opposite \ side)/(hypothenuse)= (x)/(10)`


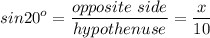
So,
`x=10\cdot sin20^o`


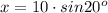
sin20° must be given, or can be found using a calculator:


Using the calculator of our pc: Calculator- view:Scientific- press 20 then sin button, we find : sin20°=0.342



`x=10\cdot sin20^o=10\cdot0.342=3.42`


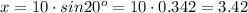
Answer: A)3.4