Question

In a songwriting competition, the minimum length of a song is 2.5 minutes. The maximum length of a song is 5.5 minutes. Write an absolute value equation that has these minimum and maximum lengths as its solutions.

Answer 1

The required absolute value equation that has these minimum and maximum lengths as its solutions is |x-4| = 1.5

Explanation:

Consider the provided information.

In a songwriting competition, the minimum length of a song is 2.5 minutes. The maximum length of a song is 5.5 minutes.

Let x is the length of song.

The range is 2.5 to 5.5

Find the mid point of the range as shown:

`(2.5+5.5)/(2)=4`

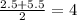
Thus, for every x the inequality holds:

2.5 = x or x = 5.5

Subtract 4 from each sides.

2.5 - 4 = x - 4 or x - 4 = 5.5 - 4

-1.5 = x - 4 or x - 4 = 1.5

This can be written as:

|x-4| = 1.5

Hence, the required absolute value equation that has these minimum and maximum lengths as its solutions is |x-4| = 1.5

Answer 2

|4 - x| < 1.5 minutes, where x = length of song
or
|x - 4| < 1.5 minutes, where x = length of song

Explanation: 4 minutes is the midpoint between 2.5 and 5.5 and is 1.5 minutes away from both 2.5 and 5.5, so the difference in the length of the song (x) and 4 minutes cannot be greater than 1.5 minutes.