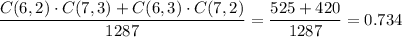Question

Rework problems 13 and 14 from section 2.4 of your textbook (page 81) about the bucket containing orange tennis balls and yellow tennis balls from which 5 balls are selected at random, but assume that the bucket contains 6 orange balls and 7 yellow balls.

1) What is the probability that, of the 5 balls selected at random, at least one is orange and at least one is yellow?
2)What is the probability that, of the 5 balls selected at random, at least two are orange and at least two are yellow?

Answer 1

The formula
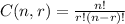`C(n, r)= (n!)/(r!(n-r)!)`, where r! is 1*2*3*...r

is the formula which gives us the total number of ways of forming groups of r objects, out of n objects.

for example, given 10 objects, there are C(10,6) ways of forming groups of 6, out of the 10 objects.

----------------------------------------------------------------------------------------------------

The bucket contains 6 orange balls and 7 yellow balls, that is a total of 13 balls.

consider the balls of the same color to be different objects (as they indeed are, don't think of them as identical)

The total number of groups of 5 balls out of the 13, that we can form is :


`\displaystyle{C(13, 5)= (13!)/(5!8!)= (13\cdot12\cdot11\cdot10\cdot9\cdot8!)/(5!8!)`


`(13\cdot12\cdot11\cdot10\cdot9)/(5\cdot4\cdot3\cdot2\cdot1)=13\cdot11\cdot9= 1287`


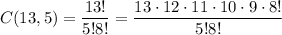
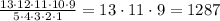1) What is the probability that, of the 5 balls selected at random, at least one is orange and at least one is yellow?

the event can happen as follows:

{1 orange, 4 yellow} or {2 orange, 3 yellow} or {3 orange, 2 yellow} or {4 orange, 1 yellow}


that is, the only cases we are not considering are {5 orange} or {5 yellow}


5 orange balls can be selected in C(6, 5) = 6!/(5!1!)=6 different ways,

and 5 yellow balls can be selected in C(7, 5)=7!/(5!2!)=(7*6)/2=21 different ways.

so 5 orange balls or 5 yellow balls can be selected in 6+21=27 different ways,


this means that P(5 orange balls or 5 yellow balls)=27/1287=0.02


P({1 orange, 4 yellow} or {2 orange, 3 yellow} or {3 orange, 2 yellow} or {4 orange, 1 yellow}) = 1-P(5 orange balls or 5 yellow balls)=1-0.02=0.98



Part 2

The event "at least two are orange and at least two are yellow " can happen in the following ways:

{2 orange, 3 yellow} or {3 orange, 2 yellow}

2 orange, 3 yellow balls can be selected in C(6,2)*C(7,3) because

any selected 2 of the 6 orange balls, can be combined with any group of 3, out of the 7 yellow balls.

so we calculate:



`\displaystyle{ C(6,2)\cdot C(7,3)= (6!)/(2!4!) \cdot (7!)/(4!3!)=15\cdot (7\cdot6\cdot5)/(3\cdot2)=525`


`\displaystyle{ C(6,3)\cdot C(7,2)= (6!)/(3!3!) \cdot (7!)/(5!2!)= (6\cdot5\cdot4)/(3\cdot2) \cdot21=420`


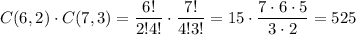
thus,

P ({2 orange, 3 yellow} or {3 orange, 2 yellow})=


P (2 orange, 3 yellow) + P (3 orange, 2 yellow)=



`\displaystyle{(C(6,2)\cdot C(7,3)+C(6,3)\cdot C(7,2))/(1287)= (525+420)/(1287)= 0.734`