Which functions are symmetric with respect to the y-axis? Check all that apply. f(x) = |x| f(x) = |x| + 3 f(x) = |x + 3| f(x) = |x| + 6 f(x) = |x – 6| f(x) = |x + 3| – 6

Question

asked Sep 21, 2018 78.2k views

2 Answers

Cambecc · Answer 1 · 2018-09-28T02:00:03+0000

Answer:

The correct options are 1, 2 and 4.

Explanation:

The vertex form of an absolute function is

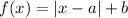
f(x)=|x-a|+b

Where, (a,b) is the vertex of the function and x=a is axis of symmetry.

The function is symmetric with respect to the y-axis. It means the axis of symmetry is x=0. It is possible if the value of a in the vertex form is 0.

In option 1,

f(x)=|x|

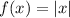
Here, a=0 and b=0.

Since the value of a=0, therefore it is symmetric with respect to the y-axis.

In option 2,

f(x)=|x|+3

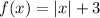
Here, a=0 and b=3.

Since the value of a=0, therefore it is symmetric with respect to the y-axis.

In option 3,

f(x)=|x+3|

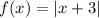
Here, a=-3 and b=0.

Since the value of a≠0, therefore it is not symmetric with respect to the y-axis.

In option 4,

f(x)=|x|+6

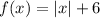
Here, a=0 and b=6.

Since the value of a=0, therefore it is symmetric with respect to the y-axis.

In option 5,

f(x)=|x-6|

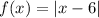
Here, a=6 and b=0.

Since the value of a≠0, therefore it is not symmetric with respect to the y-axis.

In option 6,

f(x)=|x+3|-6

Here, a=-3 and b=-6.

Since the value of a≠0, therefore it is not symmetric with respect to the y-axis.

Hence the correct options are 1, 2 and 4.