Answer:
The distance between P and T on the coordinate grid is 25 units.
Explanation:
Coordinate of P = (-10,15)
Coordinate of T = (15,15)
By distance formula we have distance between ( a,b) and (c,d) is
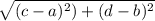
Here (a,b) = Coordinate of P = (-10,15) and (c,d) = Coordinate of T = (15,15)
Substituting

The distance between P and T on the coordinate grid is 25 units.