Answer:
The explicit equation for the given geometric sequence is
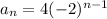 . The domain for the geometric sequence is all positive integers except 0.
. The domain for the geometric sequence is all positive integers except 0.
Explanation:
It is given that the first term of the geometric sequence is 4 and the second term is -8.
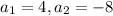
The common ratio for the sequence is
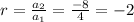
The explicit equation for a given geometric sequence is
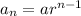
where, a is first term, n is number of term and r is common ratio.
The explicit equation for the given geometric sequence is
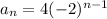
Here n is the number of term. So, the value of n is must be a positive integer except 0.
Therefore the domain for the geometric sequence is all positive integers except 0.