Question

How long will it take for a radioactive isotope with a decay constant of 0.15 (which means a half life of 4.6 days ) to decay to 5% of its original value?

Answer 1

for half lives

`A=P((1)/(2))^(t)/(h)`

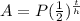
A=final amount
P=present amount
t=time in some units (this case it is days)
h=half life in days in th is case


so
given
we want 5% left
so A=5% of P or 5/100 of P or 1/20 of P or 0.05P

h=4.6

so

`0.05P=P((1)/(2))^(t)/(4.6)`
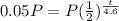
divide bth sides by P

`0.05=((1)/(2))^(t)/(4.6)`
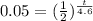
take ln of both sides

`ln(0.05)=ln((1)/(2))^(t)/(4.6)`

`ln(0.05)=((t)/(4.6))ln((1)/(2))`

`ln(0.05)=((t)/(4.6))ln((1)/(2))`
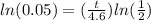
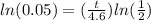
divide both sides by
`ln((1)/(2))`

`(ln(0.05))/(ln((1)/(2)))=(t)/(4.6)`
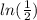
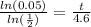
times both sides by 4.6

`(4.6ln(0.05))/(ln((1)/(2)))=t`
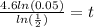
use your calculator
19.889t
so after about 20 days

Answer 2

When we are dealing with an equation like this, we know that N=No exp(-kt), where k is the decay constant, 5% of its original value means N=(5/100)No
so, for t=t', N=(5/100)No, (5/100)No=Noexp(-kt'), (5/100)=exp(-kt')
Ln(5/100)=Lnexp(-kt')= - kt', -2.99 = -0.15t', so t' = 19.93
so the answer is E 19.97 days!