Question

What is the true solution to the equation below?

2 ln e^(ln 2x)-ln e^(ln 10x)=ln 30<br />
x=30<br />
x=75<br />
x150<br />
x=300

Answer 1

yeeee

assuming your equaiton is

`2ln(e^(ln(2x)))-ln(e^(ln(10x)))=ln(30)`


remember some nice log rules

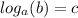
`log_a(b)=c` translates to
`a^c=b`
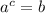
and

`a^(log_a(b))=b`
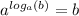
and

`xlog_c(b)=log_c(b^x)`
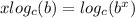
and

`ln(x)=log_e(x)`
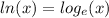
and

`log(a)-log(b)=log((a)/(b))`
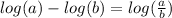
and
if
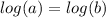
`log(a)=log(b)` then a=b

so

we can simplify a bit of stuff here

the
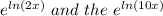
`e^(ln(2x)) \space\ and \space\ the \space\ e^(ln(10x))` can be simplified to
`2x \space\ and \space\ 10x`

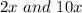
so we gots now


`2ln(2x)-ln(10x)=ln(30)`

`ln((2x)^2)-ln(10x)=ln(30)`

`ln(4x^2)-ln(10x)=ln(30)`

`ln((4x^2)/(10x))=ln(30)`
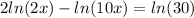
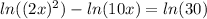
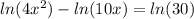
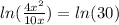
same base so

`(4x^2)/(10x)=30`

`(2x)/(5)=30`
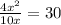
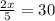
times both sides by 5

`2x=150`
divide both sides by 2

`x=75`
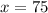
answer is x=75