yeeee
assuming your equaiton is
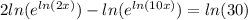
remember some nice log rules
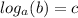
translates to
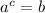
and
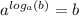
and
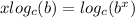
and
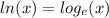
and
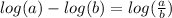
and
if
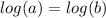
then a=b
so
we can simplify a bit of stuff here
the
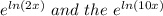
can be simplified to
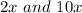
so we gots now
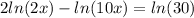
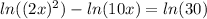
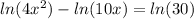
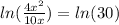
same base so
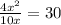
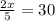
times both sides by 5
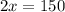
divide both sides by 2
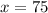
answer is x=75