to check if two vectors are orthogonal(perpendicular), simply check their dot product, if their dot product is 0, then they're perpendicular, let's check.
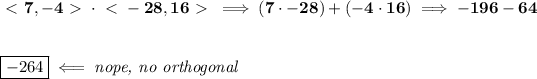
to check if two vectors are parallel, simply check their slope by doing a b/a check, if the slopes are the same, then they're indeed parallel to each other, let's check.

well, there you have it, the slopes are the same.