Question

a regular rectangular pyramid has a base and lateral faces that are congruent equilateral triangles. it has a lateral surface area of 72 square centimeters. what is the surface area of the regular triangular pyramid?

Answer 1

To find the surface area of a regular triangular pyramid, you need to find the area of the base triangle and the area of the lateral faces. The surface area of the regular triangular pyramid is the sum of the area of the base triangle and the area of the three lateral faces. The base triangle's area can be calculated using the formula for the area of a triangle.

Step-by-step explanation:

To find the surface area of a regular triangular pyramid, we need to find the area of the base triangle and the area of the lateral faces. Since the base and lateral faces are congruent equilateral triangles, the lateral surface area of the pyramid is equal to the area of the three lateral faces. Given that the lateral surface area is 72 square centimeters, each lateral face has an area of 24 square centimeters. The surface area of the regular triangular pyramid is the sum of the area of the base triangle and the area of the three lateral faces. Since the base triangle is an equilateral triangle, we can find its area using the formula for the area of a triangle: A = (1/2) x base x height. In this case, the base length and the height of the triangle are the same, so the formula becomes: A = (1/2) x side x side. The side length of the triangle can be calculated using the equation: side = square root of [(4 x lateral surface area) / (square root of 3)]. Plugging the values into the formula, the area of the base triangle is 27.71 square centimeters. Therefore, the surface area of the regular triangular pyramid is 27.71 + (3 x 24) = 99.71 square centimeters.

Answer 2

A pyramid is regular if its base is a regular polygon, that is a polygon with equal sides and angle measures.
(and the lateral edges of the pyramid are also equal to each other)

Thus a regular rectangular pyramid is a regular pyramid with a square base, of side length say x.

The lateral faces are equilateral triangles of side length x.

The lateral surface area is 72 cm^2, thus the area of one face is 72/4=36/2=18 cm^2.

now we need to find x. Consider the picture attached, showing one lateral face of the pyramid.

by the Pythagorean theorem:


`h= \sqrt{ x^(2) - (x/2)^(2)}= \sqrt{ x^(2)- x^(2)/4}= √(3x^2/4)= ( √(3) )/(2)x`

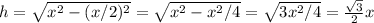
thus,


`Area_(triangle)= (1)/(2)\cdot base \cdot height\\\\18= (1)/(2)\cdot x \cdot ( √(3) )/(2)x\\\\ (18 \cdot 4)/( √(3))=x^2`

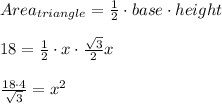
thus:


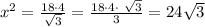
`x^2 =(18 \cdot 4)/( √(3))= (18 \cdot 4 \cdot\ √(3) )/(3)=24 √(3)` (cm^2)

but
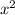
`x^(2)` is exactly the base area, since the base is a square of sidelength = x cm.


So, the total surface area = base area + lateral area =
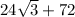
`24 √(3)+72` cm^2


Answer:
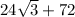
`24 √(3)+72` cm^2