a)
In general, to complete the square for ax² + bx + c:
You take out a:
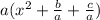
You then do like so:
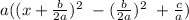
You can now tidy up and it will be in the completed-the-square form:
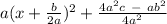
Note: The ab² term will always be negative, you never ever add the ab² term
This may look complicated but it's not really;
In the case of the actual question, for f(x), we can simply say:
a = 1
b = -2
c = -3
If you input these values into the last equation I've written you will get what your looking for:

=
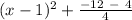
=

q = -4
b)
The completed-the-square form of the quadratic equation tells us where the lowest of highest point (the vertex) of the graph is:
The coordinates of the vertex, in general would be:
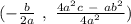
It x-coordinate of the vertex is simply the number inside the bracket next to the x term multiplied by -1;
The y-coordinate of the vertex is simply the number outside the brackets.
So for f(x):
The vertex is (1, -4)
Something to note is that if a is positive, the vertex will be the lowest point of the graph and if a is negative, the vertex will be the highest point on the curve.
So, for f(x), we said that a = 1;
this means the vertex at (1, -4) is the lowest point;
You will need to denote this on the sketch of the graph;
The y-intercept for any graph is just c, so the y-intercept (where the graph crosses the y-axis) is -3 for f(x);
This should also be denoted on your sketch;
The x-intercepts are the final things that should be denoted on your sketch;
They can be found by factorising the quadratic equation, using the quadratic formula or completing-the-square;
It's easiest to factorise it in this case;
f(x) = (x - 3)(x + 1)
You do this by inspection;
The two numbers in the brackets must multiply to give c and sum to give b;
Using this, we can tell the x-intercepts are 3, -1 (set both brackets equal to 0 and solve for x);
These also need to be denoted on you sketch;
The graph should look something like the picture