Question

How can I use the properties of integer exponents to simplify algebraic and numeric expressions ?

Answer 1

These basic properties of integer exponents can simplify algebraic and numeric expressions.

1.

`x^(m).x^(n) = x^(m+n) \\ x^(m).x^(-n) = x^(m-n)`
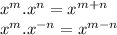
Examples:
x².x⁵ = x²⁺⁵ = x⁷
x⁸.x⁻⁵ = x⁸⁻⁵ = x³

2.

`x^(-n) = (1)/(x^(n)) \\ or \\ x^(n) = (1)/(x^(-n))`
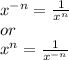
Examples:

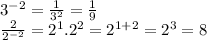
`3^(-2) = (1)/(3^(2)) = (1)/(9) \\ (2)/(2^(-2)) =2^(1).2^(2) = 2^(1+2)=2^(3)=8`

3.

`(x^(m))^(n) = x^(mn)`
Examples
(x⁴)³ = x⁴ˣ³ = x¹²
(4²)² = 4²ˣ² = 4⁴ = (2²)⁴ = 2⁸

`( (2)/(3^(2)))^(2) = (2^(2))/((3^(2))^(2)) = (2^(2))/(3^(4))`

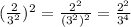
Using these basic rules makes it easier to simplify algebraic and numeric expressions.