Answer:
Point of intersection of two graph: It is defined as the point at which where both graph cut to each other.
Explanation:
We are given that f(x) and its inverse function is
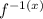 are poltted on the same coordinate plane.
are poltted on the same coordinate plane.
We have to find the point of intersection.
Point of intersection of two graph: It is defined as the point at which where both graph cut to each other and value of both functions are equal at the point.
Suppose a function
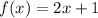
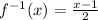
Substitute x=-1 then we get
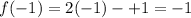
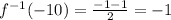
Therefore, the point of intersection is (-1,-1) because the value of both functions are equal at this point.