Question

Vector upper a overscript right-arrow endscripts has a magnitude of 69 units and points due west, while vector upper b overscript right-arrow endscripts has the same magnitude and points due south. find the magnitude and direction of (a) upper a overscript right-arrow endscripts plus upper b overscript right-arrow endscripts and (b) upper a overscript right-arrow endscripts minus upper b overscript right-arrow endscripts. specify the directions relative to due west.

Answer 1

Refer to the figure below.

Define unit vectors as follows:

`\hat{i}` in the eastern direction

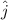
`\hat{j}` in the northern direction

Given:
Vectors a and b point due west and south respectively. Therefore

`\vec{a} = -69 \ht{i} \\ \vec{b} = -69\hat{j}`

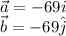
Part (a)

`\vec{a}+\vec{b}=-69\hat{i}-69\hat{j}=-69(\hat{i}+\hat{j})`
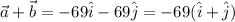
The magnitude is
|-69(√[1² + 1²])| = 69√2 = 97.58.
The direction relative to west is
θ = tan⁻¹ (b/a) = tan⁻¹ 1 = 45° south of west

Answer:
The magnitude of (a + b) is 97.58 or 69√2.
The direction is 45° south of west.

Part (b).

`\vec{a} - \vec{b} = -69\hat{i}+69\hat{j}=-69(\hat{i} -\hat{j})`
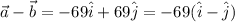
The magnitude is
|69(√(1+1)| = 69√2 = 97.58.
The direction relative to west is
tan⁻¹ (b/a) = 45° north of west.

Answer:
The magnitude of (a-b) is 97.58 or 69√2.
The direction is 45° north of west.