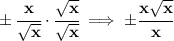f = f(x)
g = g(x)
so.. the first column has the
g expression and the second column has the
f expression and the third column has their product
a)
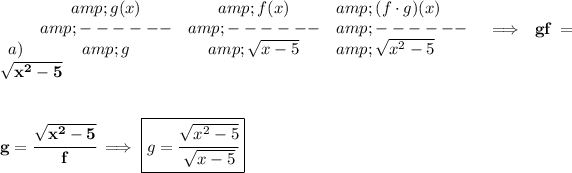
b)
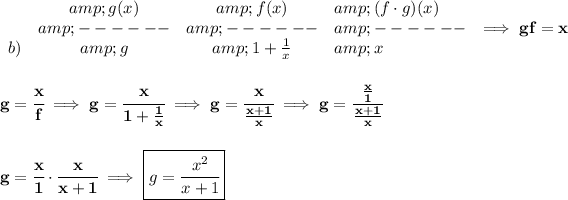
c)
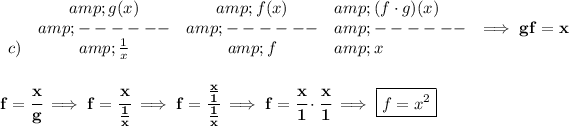
d)
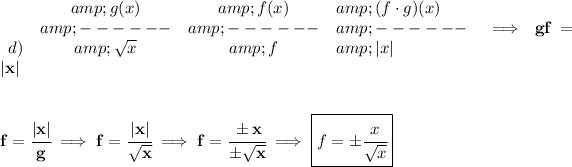
not sure if you are expected to rationalize a) and d), but we could always rationalize the denominator though
a)
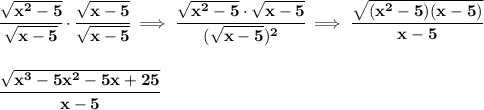
d)