i)
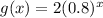
ii) the straight line joining (-7, 3) and (-3, -2), has slope
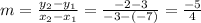 , thus the equation of the line can be written as:
, thus the equation of the line can be written as:
y-3=(-5/4)(x+7)
y-3=(-5/4)x-35/4
y=(-5/4)x-35/4+3=(-5/4)x-35/4+12/4=(-5/4)x-23/4
finally, we can write the linear function as :
f(x)=(-5/4)x-23/4
iii) line p joins the points (4, 1), (-3, -2)
we follow the same steps as in ii) to write the linear function p(x):
the slope = (-2-1)/(-3-4)=-3/-7=3/7
the equation of this line is :
y-1=(3/7)(x-4)
y-1=(3/7)x-12/7
y=(3/7)x-12/7+1=(3/7)x-12/7+7/7=(3/7)x-5/7
thus the function is
p(x)=(3/7)x-5/7
Part A:
the solution to the pair of equations y=p(x) and y=f(x) is found by equalizing y:
p(x)=f(x)
(3/7)x-5/7=(-5/4)x-23/4
(3/7)x+(5/4)x=5/7-23/4
(12+35)/28 x = (20-161)/28
47x=-141
x=-3,
substitute x=-3 in p(x) (or f(x), it is the same) to find y:
y=(3/7)x-5/7=(3/7)(-3)-5/7=-9/7 -5/7 = -14/7 = -2
thus the solution is (-3, -2)
Part B.
the solution/s of f(x) are those x for which f(x)=0,
so we solve:
f(x)=(-5/4)x-23/4 =0
(-5/4)x-23/4 =0
(-5/4)x=23/4
-5x=23
x=-23/5
THERE ARE NO 2 SOLUTIONS (or better, roots) of f(x), there is only 1.
C:
p(x)=g(x)
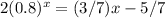
p(x) is an exponential function with the base of the exponent < 1, so it is a decreasing function. W also know that the domain is all the real numbers.
g(x) is an increasing function, the graph of it is a line that increases, because the slope = 3/7 is positive.
We can way for sure that there is a unique solution, but to find it we can only use a graphing device,
like desmos.org, used in the attached picture, or another.
graphing p(x) and g(x), we see that the intersection is at (3.707, 0.875)
So the solution is x= 3.707