Answer:
The coefficient of
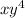 in the expension of
in the expension of
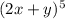 is 10.
is 10.
Explanation:
Given
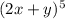 , we have to find the coefficient of
, we have to find the coefficient of
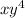 in the expension of
in the expension of
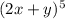 .
.
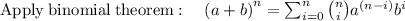
Here, a = 2x and b = y ,
Substitute above, we get,
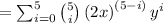
Using
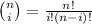
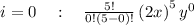
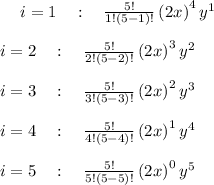
Adding all terms, we get,
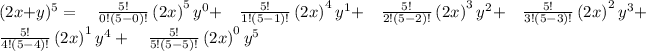
On evaluating , we get,
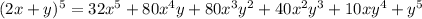
Thus, the coefficient of
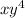 in the expension of
in the expension of
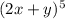 is 10.
is 10.