Answer:
(B) x equals negative 7 plus or minus the square root of sixty-five all over 2
Explanation:
The given equation is:
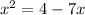
Simplifying the above equation, we have
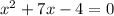
Using the Quadratic formula, we get

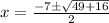
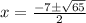
Hence, the exact solution of the given equation is x equals negative 7 plus or minus the square root of sixty-five all over 2.
Therefore, option (B) is correct.