Let the smaller number is x.
So the bigger number is x+4.
Reciprocal of smaller number is
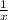
and reciprocal of larger number is
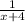
SO our equation is
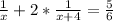
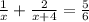

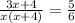
by cross multiplication rule
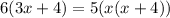



Now we can solve it by factorization.
As we can see -24*5 = -120.
So we can write -120 as 12 * (-10) = -120 because 12 - 10 = 2
SO we can write expression as

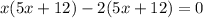

So x = 2 or x =
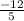
But we have to choose positive integer. SO we will choose x = 2.
SO the smaller number is 2 and bigger number is 6.