The curve
is parameterized by
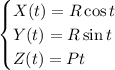
so in the line integral, we have
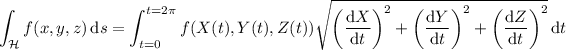
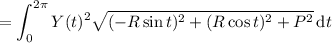


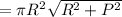
You are mistaken in thinking that the gradient theorem applies here. Recall that for a scalar function
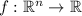
, we have gradient
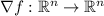
. The theorem itself then says that the line integral of
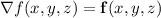
along a curve
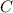
parameterized by
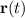
, where
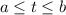
, is given by
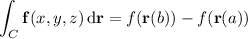
Specifically, in order for this theorem to even be considered in the first place, we would need to be integrating with respect to a vector field.
But this isn't the case: we're integrating
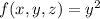
, a scalar function.