Question

Solve the problem, calculate the line integral of f along h

Answer 1

The curve
`\mathcal H` is parameterized by


`\begin{cases}X(t)=R\cos t\\Y(t)=R\sin t\\Z(t)=Pt\end{cases}`

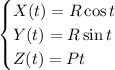
so in the line integral, we have


`\displaystyle\int_(\mathcal H)f(x,y,z)\,\mathrm ds=\int_(t=0)^(t=2\pi)f(X(t),Y(t),Z(t))\sqrt{\left((\mathrm dX)/(\mathrm dt)\right)^2+\left((\mathrm dY)/(\mathrm dt)\right)^2+\left((\mathrm dZ)/(\mathrm dt)\right)^2}\,\mathrm dt`

`=\displaystyle\int_0^(2\pi)Y(t)^2√((-R\sin t)^2+(R\cos t)^2+P^2)\,\mathrm dt`

`=\displaystyle\int_0^(2\pi)R^2\sin^2t√(R^2+P^2)\,\mathrm dt`

`=\displaystyle\frac{R^2√(R^2+P^2)}2\int_0^(2\pi)(1-\cos2t)\,\mathrm dt`

`=\pi R^2√(R^2+P^2)`

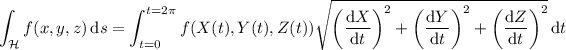
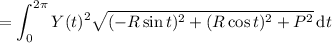
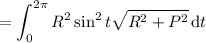
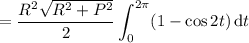
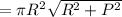
You are mistaken in thinking that the gradient theorem applies here. Recall that for a scalar function
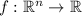
`f:\mathbb R^n\to\mathbb R`, we have gradient
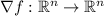
`\\abla f:\mathbb R^n\to\mathbb R^n`. The theorem itself then says that the line integral of
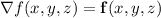
`\\abla f(x,y,z)=\mathbf f(x,y,z)` along a curve
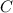
`C` parameterized by
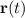
`\mathbf r(t)`, where
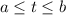
`a\le t\le b`, is given by


`\displaystyle\int_C\mathbf f(x,y,z)\,\mathrm d\mathbf r=f(\mathbf r(b))-f(\mathbf r(a))`

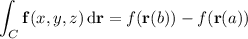
Specifically, in order for this theorem to even be considered in the first place, we would need to be integrating with respect to a vector field.

But this isn't the case: we're integrating
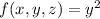
`f(x,y,z)=y^2`, a scalar function.