Question

Find the area of a triangle with legs that are: 9 mm, 6 mm, and 12 mm.

Answer 1

first find half of perimeter and name it p.
9+6+12=15+12=27
p=27/2=13.5
use this formula

`√(p(p-a)(p-b)(p-c))`
√13.5*4.5*7.5*1.5=2.25*√9*√3*√5=6.75√15

Answer 2

Answer:
`26.14\text{ mm}^2`

Explanation:

By Heron's formula ,the area of a triangle is given by :-

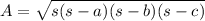`A=√(s(s-a)(s-b)(s-c))` , where s is semi-perimeter of triangle and a,b ,c are the sides of the triangle.

Given : a=9 mm, b=6 mm, and c=12 mm.

Then , semi-perimeter:
`s=(a+b+c)/(2)`

`s=(9+6+12)/(2)=13.5`

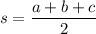
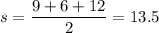
Now, the area of triangle will be :-

`A=√(13.5(13.5-9)(13.5-6)(13.5-12))\\\\\Rightarrow\ A=√(13.5\cdot4.5\cdot7.5\cdot1.5)\\\\\Rightarrow\ A=26.1426375869\text{\ mm}^2\approx26.14\text{ mm}^2`