Answer:
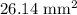
Explanation:
By Heron's formula ,the area of a triangle is given by :-
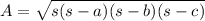 , where s is semi-perimeter of triangle and a,b ,c are the sides of the triangle.
, where s is semi-perimeter of triangle and a,b ,c are the sides of the triangle.
Given : a=9 mm, b=6 mm, and c=12 mm.
Then , semi-perimeter:
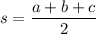
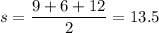
Now, the area of triangle will be :-
