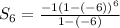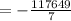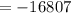Answer:
The sum of the given geometric sequence is -16807.
Explanation:
Since, the sum of a geometric sequence is,
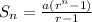 for r > 1
for r > 1
Or,
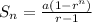 for r < 1
for r < 1
Where, a is the first term of the sequence,
n is the number of terms
And, r is the common ratio of the sequence,
Here, the given G.P.,
-1, 6, -36,.....
So, the first term is, a = -1,
And, common ratio is,

Also, n = 6,
Hence, the sum of the given geometric sequence is,