Answer:
Part A -

Part B - (h,k)=(-2,-15) , The minimum of the graph is at (-2,-15)
Part C - Axis of symmetry is x=-2
Explanation:
Given : The function
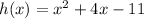 represents a parabola.
represents a parabola.
Part A -
To find : Rewrite the function in vertex form by completing the square. Show your work.
Solution :
The function
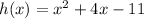
Vertex form is
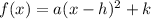
We apply completing the square in given function,
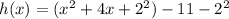

The required vertex form is

Part B -
To find : Determine the vertex and indicate whether it is a maximum or a minimum on the graph. How do you know?
Solution :
The vertex form is
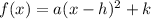
where, (h,k) are the vertex of the function
On comparing with

Vertex are (h,k)=(-2,-15)
For minimum or maximum we have to find the point
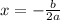
From given function a=1 and b=4
So,
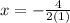

The minimum value is at x=-2
Substitute in function we get, y=-15
Therefore, The minimum of the graph is at (-2,-15)
Part C -
To find : Determine the axis of symmetry for h(x).
Solution :
Axis of the symmetry is the x-coordinate of the vertex.
So, Axis of symmetry is x=-2