Question

The function h(x) = x2 + 4x − 11 represents a parabola.

Part A: Rewrite the function in vertex form by completing the square. Show your work.

Part B: Determine the vertex and indicate whether it is a maximum or a minimum on the graph. How do you know?

Part C: Determine the axis of symmetry for h(x).

Answer 1

A.
= (x + 2)^2 - 4 - 11
= (x + 2)^2 - 15

B. vertex is at ( -2, -15) which is a minimum because the coefficient of x^2 is positive.

C. The axis of symmetry is a vertical line passing through the vertex It is
x = -2.

Answer 2

Part A -
`h(x)=(x+2)^2-15`

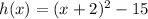
Part B - (h,k)=(-2,-15) , The minimum of the graph is at (-2,-15)

Part C - Axis of symmetry is x=-2

Explanation:

Given : The function
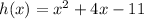`h(x)=x^2+4x-11` represents a parabola.

Part A -

To find : Rewrite the function in vertex form by completing the square. Show your work.

Solution :

The function
`h(x)=x^2+4x-11`

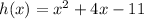
Vertex form is
`f(x)=a(x-h)^2+k`

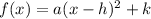
We apply completing the square in given function,

`h(x)=(x^2 + 4x + 2^2)-11-2^2`

`h(x)=(x+2)^2-15`

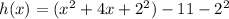
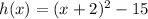
The required vertex form is
`h(x)=(x+2)^2-15`

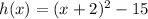
Part B -

To find : Determine the vertex and indicate whether it is a maximum or a minimum on the graph. How do you know?

Solution :

The vertex form is
`f(x)=a(x-h)^2+k`

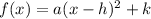
where, (h,k) are the vertex of the function

On comparing with
`h(x)=(x+2)^2-15`

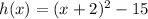
Vertex are (h,k)=(-2,-15)

For minimum or maximum we have to find the point
`x=-(b)/(2a)`

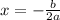
From given function a=1 and b=4

So,
`x=-(4)/(2(1))`

`x=-2`

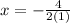
The minimum value is at x=-2

Substitute in function we get, y=-15

Therefore, The minimum of the graph is at (-2,-15)

Part C -

To find : Determine the axis of symmetry for h(x).

Solution :

Axis of the symmetry is the x-coordinate of the vertex.

So, Axis of symmetry is x=-2