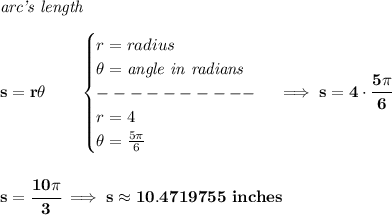
well, we know the minute hand is 4 inches long, thus, the radius of the circular clock is 4 then :)
part 1)
now, there are 360° in a circle.... the clock has 60 minutes, or 60 even intervals...now, how many degrees is it for each minute? well, let's divide 360° by 6 then, 360/6 is just 6. That means each minute to the next, is 6°, well, how many radians is that? well, we know there are π radians in 180°, so, how many radians in 6° then?
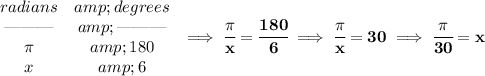
so, there are π/30 radians in 6°.
now, from 1:25 to 1:50 is 25 minutes, and thus 25 * π/30 radians, or 5π/6 radians.
part 2)
what is the arc made by those 25 minutes?