Question

What is a1 of the arithmetic sequence for which a3=126 and a64=3,725

Answer 1

d=an-am/n-m
d=a64-a3/64-3
d=3725-126/61=59
a3=a1+2d
126=a1+118
a1=8

Answer 2

Answer: The required value of the first term is 8.

Step-by-step explanation: We are given to find the first term of the arithmetic sequence for which the third term is 126 and sixty fourth term is 3725.

We know that

the nth term of an arithmetic sequence with first term a and common difference d is given by

`a_n=a+(n-1)d.`

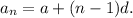
According to the given information, we have

`a_(3)=126\\\\\Rightarrow a+(3-1)d=126\\\\\Rightarrow a+2d=126~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

and

`a_(64)=3725\\\\\Rightarrow a+(64-1)d=3725\\\\\Rightarrow a+63d=3725~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

Subtracting equation (i) from equation (ii), we get

`(a+63d)-(a+2d)=3725-126\\\\\Rightarrow 61d=3599\\\\\Rightarrow d=59.`

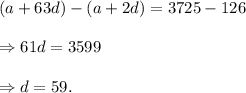
From equation (i), we get

`a+2*59=126\\\\\Rightarrow a=126-118\\\\\Rightarrow a=8`

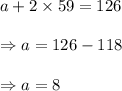
Thus, the required value of the first term is 8.