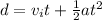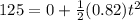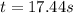Answer:
Part a)
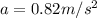
Part b)
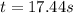
Step-by-step explanation:
Part a)
Maximum tension that is obtained by the rope is 2.5 times the weight of the rope
So here we know that
mass of the boulder = 750 kg
mass of the chain = 575 kg
now total mass of the boulder and chain = 750 kg + 575 kg
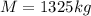
Now we have maximum tension in the rope is given as
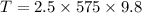

now from Newton's 2nd law we have
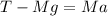
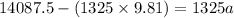
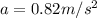
Part b)
Time taken by the boulder to raise by 125 m depth
we can use kinematics and we will assume here that it will start from rest and accelerate at above maximum value that we found in part a)
so by kinematics